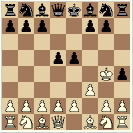
move 4 by discovered check

| final position |

|
|
black checkmating on move 4 by discovered check |
I thought about a generalization of the well known construction task "Construct a game which ends with black delivering checkmate on move 2", where the black queen checkmates on h4.
The question was:
What is the shortest number of moves needed for checkmating from the initial position with any given black piece?
[If you are dying to see the interactive answers you may have a look here ...]
[New: Shortest construction tasks map]
After having found solutions for all 16 different cases I wrote a computer program to compute all possible games of 3 and 4 moves and found more than 10000 different mates within 3 moves and more than 9 million different mates within 4 moves. I got some surprises in having not found the shortest possible mates for four of the eight pawn problems by myself.
Then I realized the additional construction tasks of "double checkmate" and "discovered checkmate" (the second appears as a solution for mating with the black king e8, but on move 5 instead optimally on move 4).
Among all checkmates within 4 moves I found exactly 4 games with a discovered checkmate (a problem from Sam Loyd published in Le Sphinx, 1866, mentioned in the above links), and none with a double checkmate.
The notion [5+2+2=9] defines, that there are exactly 9 different games possible for the given problem. These 9 different games are divided into 5 different games with a same first ending position, 2 different games with a same second ending position and 2 different games with a same third ending position. The problem characterized [unique] is the only unique problem within these 18 problems! The bracket notion is only applied to problems with less than 10 different solutions.
That is all -- the problems from below may be played interactively -- have a lot of fun!.
Construct a game which ends with:
|
Black checkmating on move ... |
||
|
... 4 - by discovered check [2+2=4]. ... 5 - with pawn a7. ... 4 - with pawn b7 [unique]. ... 4 - with pawn c7 [5+2+2=9]. ... 4 - with pawn d7. ... 4 - with pawn e7. ... 4 - with pawn f7 [2+3=5]. ... 4 - with pawn g7 [3+3+3=9]. ... 5 - with pawn h7. |

|
... 5 - by double check. ... 5 - with rook a8. ... 3 - with knight b8. ... 4 - with bishop c8. ... 2 - with queen d8 [2+2+2+2=8]. ... 5 - with king e8. ... 3 - with bishop f8. ... 4 - with knight g8. ... 5 - with rook h8. |