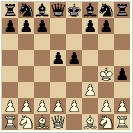
Zug 4 durch Abzugschach
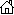

| Schlussstellung |

|
|
Schwarz setzt matt in Zug 4 durch Abzugschach |
Ich habe über eine Generalisierung der bekannten Konstruktionsaufgabe "Konstruiere eine Schachpartie, in welcher Schwarz in Zug 2 matt setzt" nachgedacht, in welcher die schwarze Dame auf h4 matt setzt.
Die Frage war nun:
Was ist die kürzeste notwendige Anzahl von Zügen um mit jeder schwarzen Figur aus der Ausgangsstellung matt zu setzen?
[Wenn es unter den Nägeln brennt, die interaktiven Antworten zu sehen, findet man sie hier ...]
[Neu: Kürzeste Konstruktionsaufgaben-Karte]
Nachdem ich Lösungen für alle 16 verschiedenen Fälle gefunden hatte, schrieb ich ein Computerprogramm, um alle möglichen Partieen mit 3 und 4 Zügen zu berechnen, und fand mehr als 10000 verschiedene Schachmatts in 3 Zügen und mehr als 9 Millionen verschiedene Schachmatts in 4 Zügen. Ich war überrascht, dass ich für vier der acht Bauernprobleme nicht die kürzeste Lösung gefunden hatte.
Dann erkannte ich die zusätzlichen Konstruktionsaufgaben "Doppelschachmatt" und "Abzugsschachmatt" (das zweite taucht auch als Lösung der Konstruktionsaufgabe für den schwarzen König e8 auf, aber dort im 5. Zug anstelle optimal im 4. Zug).
Unter allen Schachmatts mit 4 Zügen fand ich exakt 4 Partieen mit einem Abzugsschachmatt (ein Problem von Sam Loyd, veröffentlicht in Le Sphinx, 1866, was in den obigen Links auch erwähnt ist), und keines mit einem Doppelschachmatt.
Die Notation [5+2+2=9] definiert, dass genau 9 verschiedene Partieen für das gegebene Problem existieren. Diese 9 verschiedenen Partieen lassen sich in 5 verschiedene Partieen mit einer ersten Mattposition, 2 verschiedene Partieen mit einer zweiten Mattposition und 2 verschiedene Partieen mit einer dritten Mattposition aufteilen. Das mit [unique] bezeichnete Problem ist das einzige eindeutige Problem unter diesen 18 Problemen! Die Klammernotation wird nur auf Probleme angewandt, welche weniger als 10 verschiedene Lösungen besitzen.
Das ist Alles -- die nachfolgenden Probleme können interaktiv gespielt werden -- Viel Spass dabei!.
Konstruiere eine Schachpartie, welche folgendermaßen endet:
|
Schwarz setzt matt in Zug ... |
||
|
... 4 - durch Abzugsschach [2+2=4]. ... 5 - mit Bauer a7. ... 4 - mit Bauer b7 [unique]. ... 4 - mit Bauer c7 [5+2+2=9]. ... 4 - mit Bauer d7. ... 4 - mit Bauer e7. ... 4 - mit Bauer f7 [2+3=5]. ... 4 - mit Bauer g7 [3+3+3=9]. ... 5 - mit Bauer h7. |

|
... 5 - durch Doppelschach. ... 5 - mit Turm a8. ... 3 - mit Springer b8. ... 4 - mit Läufer c8. ... 2 - mit Dame d8 [2+2+2+2=8]. ... 5 - mit König e8. ... 3 - mit Läufer f8. ... 4 - mit Springer g8. ... 5 - mit Turm h8. |